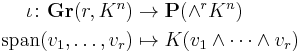Plücker embedding

In mathematics, the Plücker embedding describes a method to realize the Grassmannian of all r-dimensional subspaces of a vector space V as a subvariety of the projective space of the rth exterior power of that vector space, P(∧^r V).

The Plücker embedding was first defined, in the case r = 2, n = 4, in coordinates by Julius Plücker as a way of describing the lines in three dimensional space (which, as projective lines in real projective space, correspond to two dimensional subspaces of a four dimensional vector space). This was generalized by Hermann Grassmann to arbitrary r and n using a generalization of Plücker's coordinates, sometimes called Grassmann coordinates.

Definition

The Plücker embedding (over the field K) is the map ι defined by

$\begin{align} \iota \colon \mathbf{Gr}(r, K^n) &{}\rightarrow \mathbf{P}(\wedge^r K^n)\\ \operatorname{span}( v_1, \ldots, v_r ) &{}\mapsto K( v_1 \wedge \cdots \wedge v_r ) \end{align}$

where Gr(r, Kⁿ) is the Grassmannian, i.e., the space of all r-dimensional subspaces of the n-dimensional vector space, Kⁿ.

This is an isomorphism from the Grassmannian to the image of ι, which is a projective variety. This variety can be completely characterized as an intersection of quadrics, each coming from a relation on the Plücker (or Grassmann) coordinates that derives from linear algebra.

References

Griffiths, Phillip; Harris, Joseph (1994), Principles of algebraic geometry, Wiley Classics Library, New York: John Wiley & Sons, ISBN 978-0-471-05059-9, MR 1288523